Continuous Random Variable Example

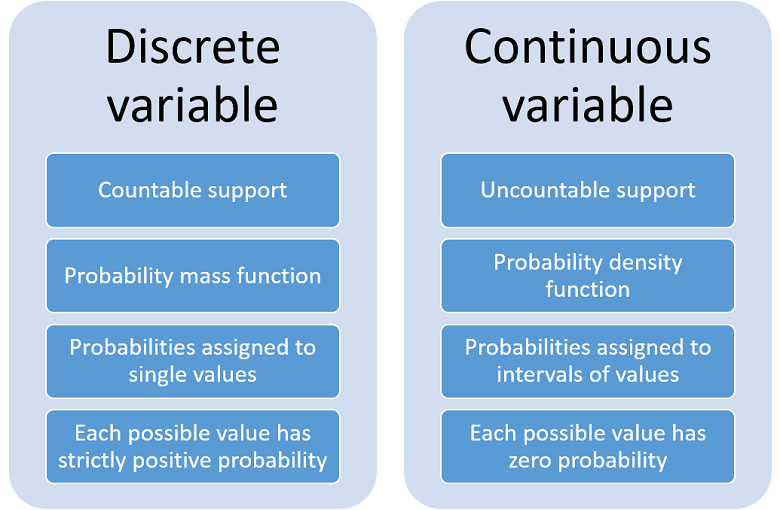
By Tia_23Drew 22 Sep, 2022 Post a Comment

A random variable X is continuous if possible values comprise either a single interval on the number line or a union of disjoint intervals. Financiers typically model stock prices and interest rates as continuous processes in continuous time.

Continuous Random Variable Detailed W 7 Examples

A variable which can only assume a countable number of real values ie the value of the discrete random sample is discrete in nature.

. For example the probability of each dice outcome is 16 because the outcomes are of equal probabilities. Continuous Random Variables can be either Discrete or Continuous. The probability density function gives the probability that any value in a continuous set of values.

What is the probability that. For other types of continuous random variables the PDF is non-uniform. Working through examples of both discrete and continuous random variables.

A random variable can be categorized into two types. An absolutely continuous random variable is a random variable whose probability distribution is absolutely continuous. For example suppose X denotes the length of time a commuter just arriving at a bus stop has to wait for the next bus.

The probability density function or PDF of a continuous random variable gives the relative likelihood of any outcome in a continuum occurring. In this article I will show you how to generate random variables both discrete and continuous case using the Inverse Transform method in Python. This is not the case for a continuous random variable.

In a continuous time context the value of a variable y at an unspecified point in time is denoted as yt or when the meaning is clear simply as y. May be depth measurements at randomly chosen locations. The range for X is the minimum depth possible to the maximum depth possible.

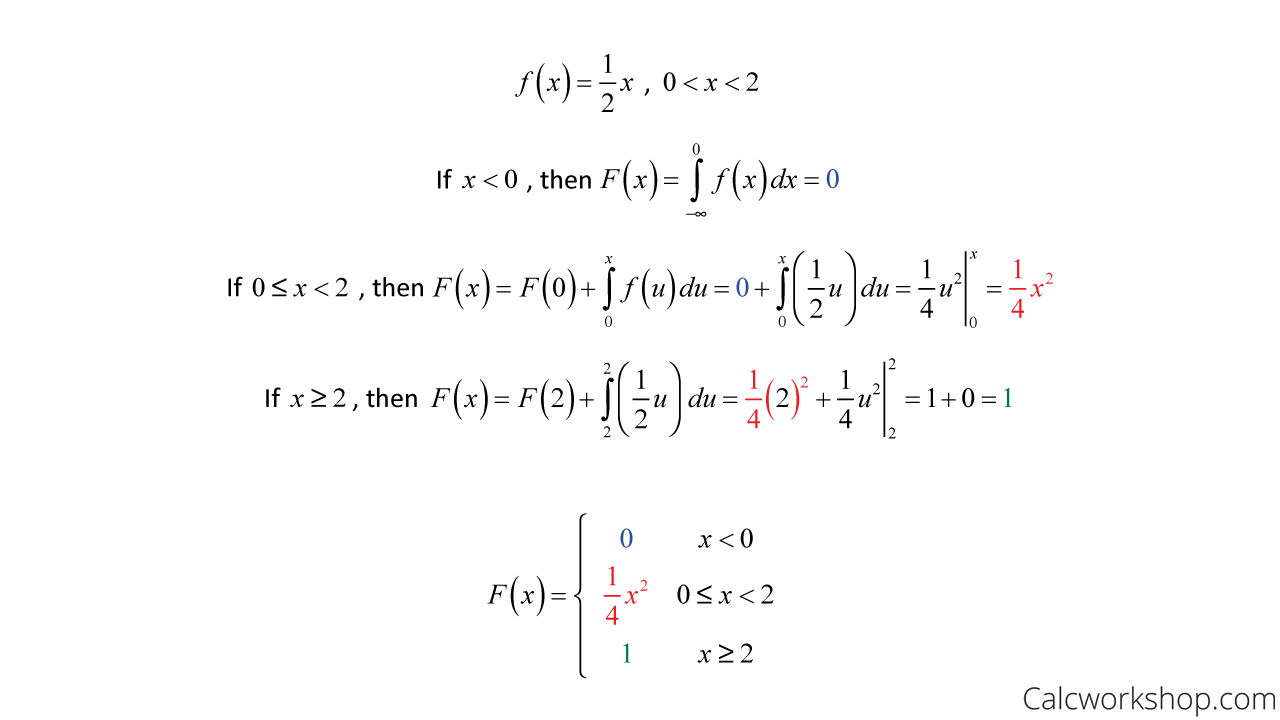
Suppose that we want to generate random variable X where the Cumulative Distribution Function CDF is. A probability mass function is used to describe the probability distribution of a discrete random variable. Random Variables A random variable usually written X is a variable whose possible values are numerical outcomes of a random phenomenonThere are two types of random variables discrete and continuous.

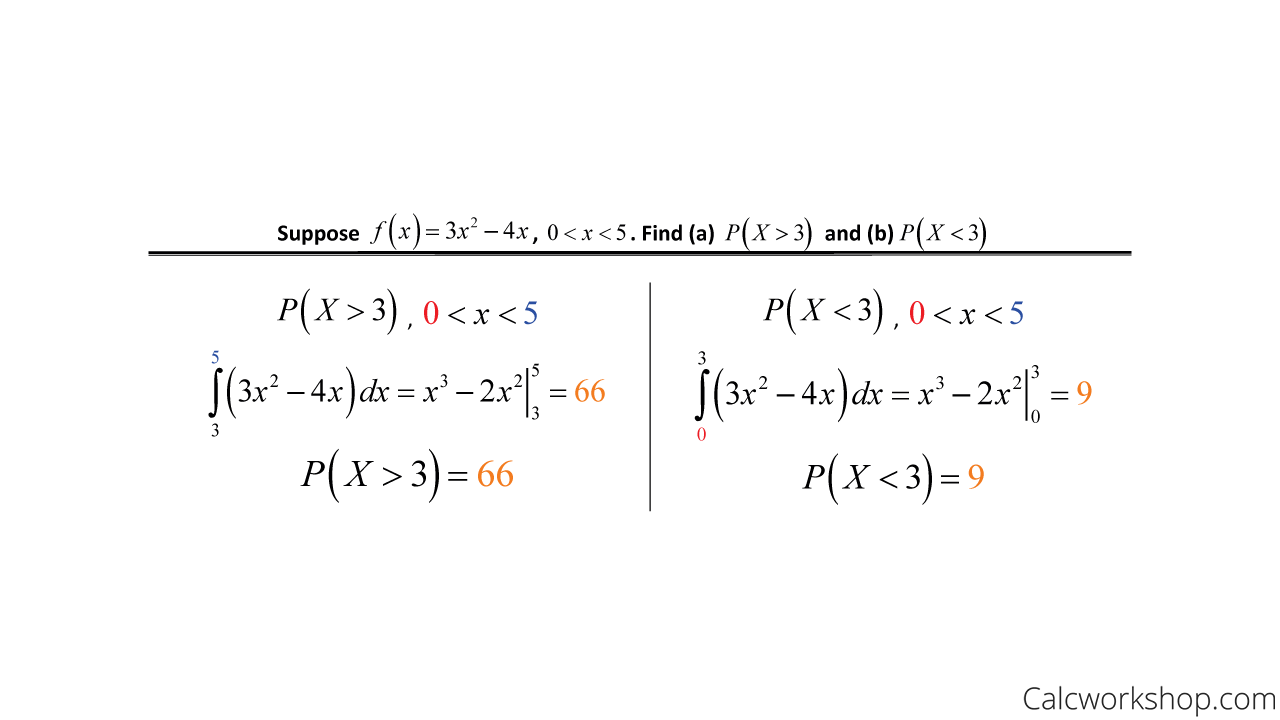
For this reason we only talk about the probability of a continuous random variable taking a value in an INTERVAL not at a point. Defining discrete and continuous random variables. This does not mean that a continuous random variable will never equal a single value only that we do not assign any probability to single values for the random variable.

Then Y jXjhas mass function f Yy ˆ 1 2n1 if x 0. Then the smallest value of X will be equal to 2 which is a result of the outcomes 1 1 2 and the highest value would be 12 which is resulting from the. But we also have random processes in continuous time where there is one random variable for each instant in time arranged as a continuum.

Working through examples of both discrete and continuous random variables. X is the Random Variable The sum of the scores on the two dice. Discrete time makes use of difference equations also known as recurrence relations.

Defining discrete and continuous random variables. Difference between random variable and random process For example we can collect the random signal. Unlike discrete variables continuous random variables can take on an infinite number of possible values.

We rst consider the case of gincreasing on the range of the random variable X. Discrete Data can only take certain values such as 12345 Continuous Data can take any value within a range such as a persons height. The uniform distribution is the simplest continuous random variable you can imagine.

For example suppose has a uniform distribution between 0 and 1. Continuous probability distribution of mens heights. If youre seeing this message it means were having trouble loading external resources on our website.

Then X is a continuous rv. One of the examples of a continuous variable is the returns of. Discrete Random Variables A discrete random variable is one which may take on only a countable number of distinct values such as 01234.

Unlike the case of discrete random variables for a continuous random variable any single outcome has probability zero of occurring. But although the number 7211916 is a possible value of X. For example lets say you had a continuous probability distribution for mens heights.

Let Xbe a uniform random variable on f n. To construct a random Bernoulli variable for some. Notice the different uses of X and x.

Types of equations Discrete time. If in the study of the ecology of a lake X the rv. An example known as the logistic map or logistic equation is.

The idea of the inverse. Random variables could be either discrete or continuous. Realizations of any random variable can be generated.

The probability that a particular random variable will equal a certain value is zero. In probability a real-valued function defined over the sample space of a random experiment is called a random variableThat is the values of the random variable correspond to the outcomes of the random experiment. And whether or not the endpoints of the interval are included does.

If buses run every 30 minutes without fail then the set of possible values of X is the interval denoted 030 the set of all decimal numbers between 0 and 30. The value of the random variable depends on chance. X is a value that X can take.

Suppose 2 dice are rolled and the random variable X is used to represent the sum of the numbers. Given random variable U where U is uniformly distributed in 01. Fig42 - PDF for a continuous random variable uniformly distributed over ab.

As the name suggests this variable is not connected or continuous. 2 Continuous Random Variable The easiest case for transformations of continuous random variables is the case of gone-to-one. Note that the total probability outcome of a discrete variable is equal to 1.

2 2n1 if x6 0. What is Random Variable in Statistics.

Continuous Random Variable Detailed W 7 Examples